自2015年 Deepbind (1)和DeepSEA (2) 这两份开拓性的工作发表以来,卷积神经网络 (CNN) 就已被广泛用于组学数据的序列分类和机制挖掘 (3–5)。然而,CNN的计算过程缺乏一个直观而精确的生物解释,因而常被视作机理不明的黑箱 (black-box);这导致人们难以从训练好的CNN模型中准确解读具有分类效力的序列特征,更不用说设计具有直观解释的新型CNN模型了。近年来虽有一些工作尝试解决此问题、并进而试图解释其生物学含义(例如SpliceRover (3) 利用 DeepLIFT (6) 对模型中学到的信息进行可视化),但他们主要以启发式的思路评估不同输入对模型中神经元激活效果的差异,并未能够准确解释CNN的计算过程。
我们之前注意到,在DeepBind等CNN模型的卷积网络结构中,其核心计算之一:卷积核扫描实际上是一个一维滑动窗口过程。而且,卷积核与位置权重矩阵(Position weight matrix, PWM)有深刻的联系:在假定输入序列以one hot-encoding形式编码的前提下(图1A),如果卷积核取成位置特异概率的对数的话,那么卷积得分就是对数似然(图1B);如果卷积核取成位置特异概率与背景概率的对数似然比(通常权重矩阵就是这样定义),那么卷积得分就是对数贝叶斯因子,描述了序列片段是更像信号还是更像随机序列(图1C)。这种联系在邓明华老师《生物信息统计模型》课件中已被明确指出来了。
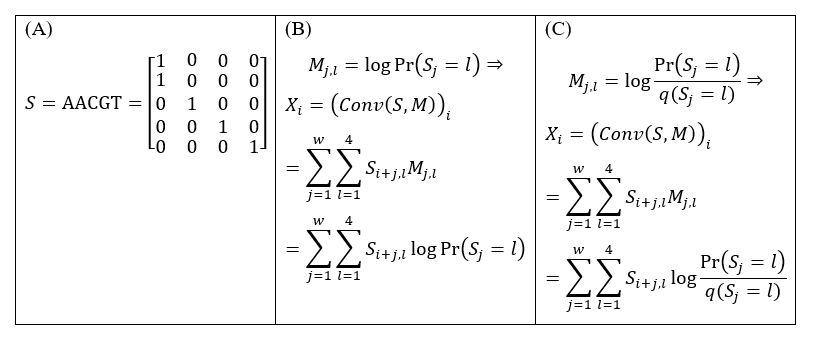
图1:当卷积核恰巧为PWM时,卷积得分即等于PWM的对数似然(或对数贝叶斯因子)。(A)以one hot-encoding编码的序列S。(B)如果卷积核M取成某PWM位置特异概率的对数,那么M在S的第i位的卷积得分Xi就是相应PWM在同位置的对数似然。(C)如果卷积核M取成某PWM位置特异概率与背景概率的对数似然比,那么M在S的第i位的卷积得分Xi就是相应PWM在同位置的对数贝叶斯因子。
与此同时,丁阳博士给出了一般卷积核的卷积得分与PWM对数似然之间的严格定量等价关系 (7)(图2A):给定卷积核在给定序列上的卷积得分,刚好严格等于某固定常数与“某一可通过该卷积核显式变换出的PWM(图2B)在同序列上的对数似然”之和。相比图1的解释,这一解释并不需要卷积核的元素是概率对数,从而可以适用于任意处理one hot-encoding输入序列的CNN模型。
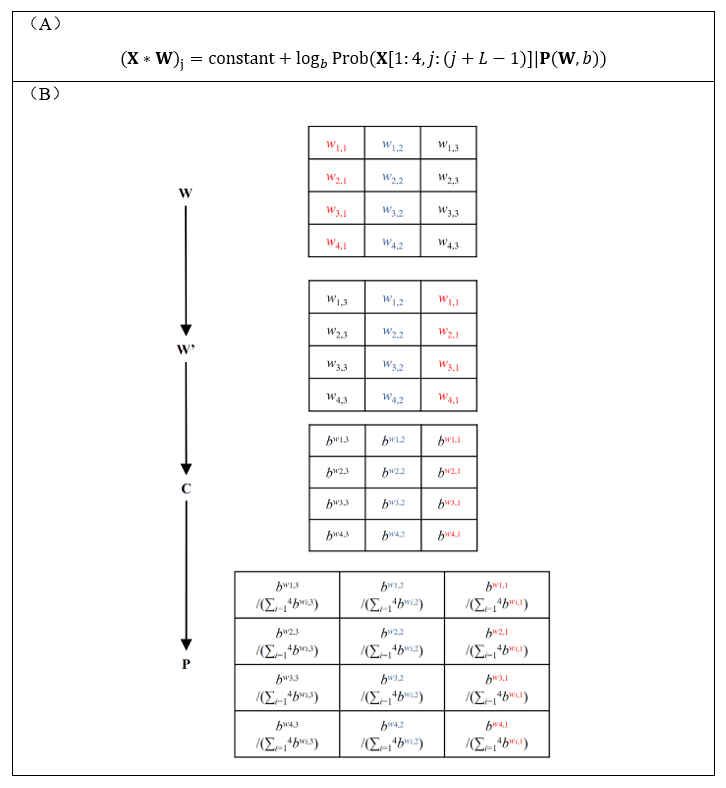
图2:一般CNN模型的任意卷积核均存在严格等价的PWM解释。(A)对于任意的序列X和卷积核W,其卷积值等于某固定常数与“某一可通过该卷积核显式变换出的PWM在同序列上的对数似然”之和。(B)通过卷积核W显式变换出该PWM的具体流程。其中b是任意大于1的常数。
基于这一针对卷积核的定量概率解释,我们结合 90年代motif finding 领域的经典 EM 算法 (8) 设计了新的 Pooling 层(期望池化, Expectation Pooling或简称“ePooling”)来代替原来模型中的全局最大池化 (9)(图3A,图3B)。这种“期望池化”的概念是受到EM算法中E 步启发而生,同时从统计上也可以理解为是传统全局最大池化(Global Max Pooling)的一种变形,即计算的是各卷积得分的“Soft” maximum 。结合前述卷积得分与PWM对数似然的关联 (7),我们证明了ePooling结果严格等价于相应PWM生成概率似然的期望,也即严格对应 EM 算法中的E步(图3C)。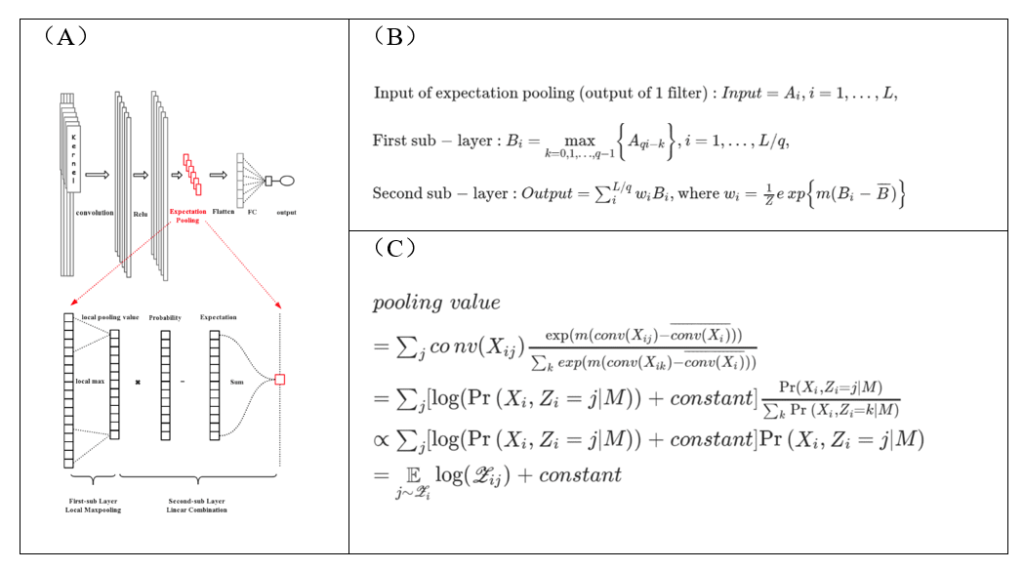
图3:期望池化(ePooling)具有直观准确的解释。(A)ePooling的设计示意图。(B)ePooling内在计算公式。(C)ePooling的结果严格等价于相应PWM生成概率的期望。
在模拟数据集上评估的结果表明,相比传统的Max Pooling和Average Pooling,ePooling能明显提高模型预测准确度、并增加模型鲁棒性(图4A),同时相对于Max Pooling而言能够有效减少模型过拟合(图4B)。同时,在690个真实ChIP-seq数据集上评估的结果也表明,ePooling能够在绝大多数数据集上有效提升使用传统Max Pooling的CNN模型的预测准确度(表1)。
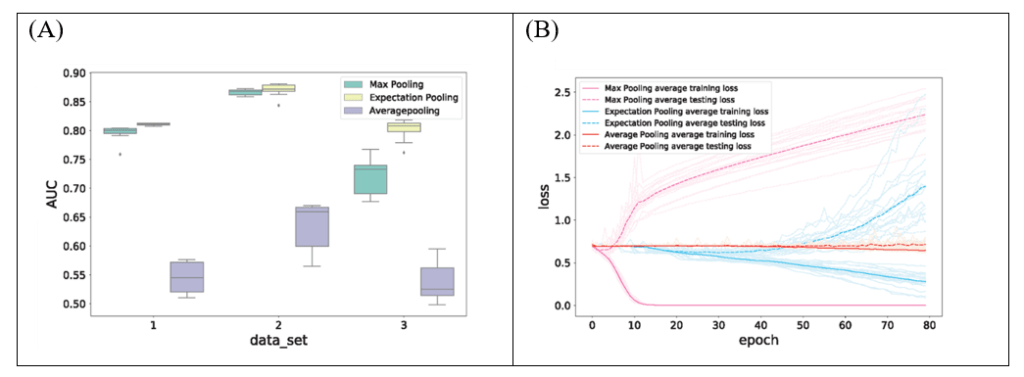
图4:ePooling在模拟数据集上有良好表现。(A)相比传统的Max Pooling和Average Pooling,ePooling能明显提高模型预测准确度(以AUC呈现)、并增加模型鲁棒性。(B)相对于Max Pooling而言,ePooling能够有效减少模型过拟合。
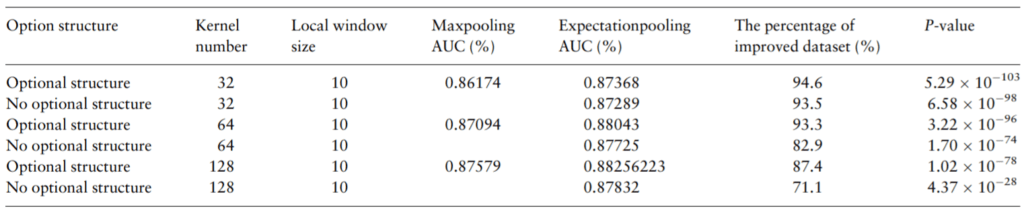
表1:相对于使用传统Max Pooling的CNN模型,ePooling在690个真实ChIP-Seq数据集中的绝大部分数据集上能够明显提升CNN模型的预测准确度(以AUC呈现)。
CNN已经成为当今生物信息学和组学研究中的有力工具。ePooling从概率可解释性出发、通过理性设计(rational design)改进了当前主流池化方法,既改善了模型的表现效果,也有助于研究者从统计学习角度更好理解潜在的生物序列模式,同时还在概率层面上提供了一些有趣的思路。我们相信,统计学习与深度学习的结合有助于将“黑箱”变成“白箱”,即发展出解释能力更强的深度学习模型,从而帮助研究者发现更为复杂的生物学规律。
本研究系与北京大学数学科学学院/定量生物学中心邓明华教授课题组合作完成,并于2019年10月9日以 Expectation pooling: an effective and interpretable pooling method for predicting DNA–protein binding 为题在线发表于Bioinformatics。博士生罗霄(北京大学数学科学学院)、本科生屠鑫明(北京大学生命科学学院)为共同第一作者,邓明华教授、高歌研究员为通讯作者。丁阳博士在前期想法讨论和文章修订上提供了大力支持。
原文链接: https://academic.oup.com/bioinformatics/advance-article/doi/10.1093/bioinformatics/btz768/5584233
代码: https://github.com/gao-lab/ePooling
参考文献:
- Alipanahi B, Delong A, Weirauch MT, Frey BJ. Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat Biotechnol. 2015 Aug;33(8):831–8.
- Zhou J, Troyanskaya OG. Predicting effects of noncoding variants with deep learning–based sequence model. Nat Methods. 2015 Oct;12(10):931–4.
- Zuallaert J, Godin F, Kim M, Soete A, Saeys Y, De Neve W. SpliceRover: interpretable convolutional neural networks for improved splice site prediction. Hancock J, editor. Bioinformatics. 2018 Dec 15;34(24):4180–8.
- Kelley DR, Snoek J, Rinn JL. Basset: learning the regulatory code of the accessible genome with deep convolutional neural networks. Genome Res. 2016 Jul;26(7):990–9.
- Ben-Bassat I, Chor B, Orenstein Y. A deep neural network approach for learning intrinsic protein-RNA binding preferences. Bioinformatics. 2018 Sep 1;34(17):i638–46.
- Shrikumar A, Greenside P, Kundaje A. Learning Important Features Through Propagating Activation Differences. ArXiv170402685 Cs [Internet]. 2019 Oct 12 [cited 2019 Dec 5]; Available from: http://arxiv.org/abs/1704.02685
- Ding Y, Li J-Y, Wang M, Tu X, Gao G. An exact transformation for CNN kernel enables accurate sequence motif identification and leads to a potentially full probabilistic interpretation of CNN [Internet]. Bioinformatics; 2017 Jul [cited 2019 Dec 5]. Available from: http://biorxiv.org/lookup/doi/10.1101/163220
- Lawrence CE, Reilly AA. An expectation maximization (EM) algorithm for the identification and characterization of common sites in unaligned biopolymer sequences. Proteins Struct Funct Genet. 1990;7(1):41–51.
- Luo X, Tu X, Ding Y, Gao G, Deng M. Expectation pooling: an effective and interpretable pooling method for predicting DNA–protein binding. Hancock J, editor. Bioinformatics. 2019 Oct 9;btz768.